Métrologie dimensionnelle. Première partie : spécifications du plan
PREAMBULE
Dans le milieu des mécaniciens amateurs, je croise souvent des gens très mal informés qui sont persuadés qu'ils sont capables de tenir des tolérances d'un centième de millimètre avec des machines de DIY posées sans précaution sur un établi de fortune. Certains vont même jusqu'à me parler de microns.
Faut-il préciser que même si je fais semblant de les écouter, je ne crois pas un mot de ce qu'ils me racontent. Et je les crois d'autant moins que leur seul instrument de mesure est un pied à coulisse numérique à vingt Euros (on y reviendra dans les pages suivantes...)
Ce qui suit a pour but, si ce n'est de remettre complètement les pendules à l'heure de montrer à quel point il est difficile de réaliser la quasi-perfection que ces affabulateurs prétendent maîtriser.
Nous allons dans cette première partie aborder rapidement les différentes tolérances géométriques car j'ai constaté que l'immense majorité des amateurs (et hélas nombre de professionnels formés sur le tas) ne savent pas interpréter les indications portées sur un plan. Il y a déjà là beaucoup de notions à bien comprendre avant d'aller plus loin. On va aborder ça très vite, juste pour vous donner envie d'aller chercher plus d'informations sur Internet. Les sites d'écoles d'ingénieurs et de lycées techniques ne manquent pas d'informations. encore faut-il avoir conscience que ces informations sont utiles et disponibles. C'est ce que je vous propose ici.
Une fois les principes de cotation bien compris, on pourra parler des moyens de contrôle, de leur capabilité, de leur utilisation.
LES DIFFERENTES TOLERANCES UTILISEES EN COTATION FONCTIONNELLE
Qu'est-ce que la cotation fonctionnelle ?
La cotation fonctionnelle est un moyen de définition des pièces qui doit permettre au mécanisme de fonctionner correctement. Selon les assemblages, on recherchera à obtenir des jeux ou des serrages plus ou moins importants entre les différentes pièces, on pourra aussi rechercher des localisations plus ou moins précises, une précision de forme ou de position relative entre deux surfaces ou pièces assemblées. La cotation fonctionnelle s'intéresse aussi à la rugosité des surfaces obtenues. C'est le bureau d'étude qui définit les besoins. Généralement, les mécaniciens amateurs ne font pas appel à un bureau d'études et se contentent de définir eux-mêmes ce qu'ils estiment nécessaire au bon fonctionnement. Ils en sont parfaitement capables à condition de bien maîtriser les tenants et aboutissants.
Tolérances dimensionnelles
Une tolérance dimensionnelle est définie entre deux surfaces d'une pièce. Déjà, à ce stade beaucoup de mécaniciens font une interprétation inexacte. En effet, il existe trois types de surfaces :
La surface idéale
La surface idéale, c'est celle qui est dessinée sur le plan. Elle est définie (implicitement) par une équation mathématique. Par exemple, une sphère est l'ensemble des points qui se trouvent à une distance donnée d'un point appelé centre, un cylindre de révolution est l'ensemble des points qui se trouvent à une distance donnée d'un axe idéal (donc parfaitement rectiligne).
La surface réelle
La surface réelle est celle qu'on obtient sur la pièce. Elle n'est jamais exactement la surface idéale. sa définition est entachée d'erreurs : de rugosité, de forme, de position. Par exemple, dans le cas du cylindre, la surface réelle peut présenter des défauts de rectitude de génératrices, des défauts de conicité, des défauts de cylindricité, des défauts de circularité dans un plan de coupe perpendiculaire à l'axe. En pratique aussi petits soient-ils, ces défauts existent toujours.
La surface modélisée
La surface modélisée est la surface qui est définie par le moyen de mesure. Aussi fiables soient les instruments utilisés, il y a toujours des erreurs au moment de la mesure. Ces erreurs (on y reviendra) peuvent être dues à différents facteurs : instrument faux, instrument mal employé, pièce dans des conditions non appropriées (dilatée par la température, déformée par la gravité, etc., par exemple) Mais aussi dues au traitement des informations relevées. Ces erreurs de traitement sont fréquentes avec les machines à mesurer tridimensionnelles. En effet, les machines relèvent un nuage de points et calculent des moyennes. Les machines utilisent différents algorithmes statistiques pour réaliser les calculs. La méthode de moindres carrés est l'une des plus employées. Mais ce n'est pas la seule. Que la mesure soit automatique ou manuelle, elle sera toujours entachée d'erreurs de traitement des données.
Lien concernant cette méthode : Lien
Si vous n'aimez pas vraiment les mathématiques, cet article de Wikipédia vous semblera incompréhensible. Ce n'est pas grave. Ce qu'il faut comprendre, c'est que cette méthode s'appuie sur deux choses fondamentales :
- des resultats de mesures
- un a-priori sur ce qu'on cherche plan, cylindte, cone, sphere, etc. )
L'algorithme, qu'il soit utilisé manuellement ou informatiquement va permettre de definir la surface ideale présupposée qui s'approche le plus de la surface réelle. On pourra connaitre les ecarts entre réelle et calculée. Il est bien evident que si au départ on se trompe d'hypothèse, les résultats n'auront aucun sens. Par exemple, si on mesure un tronc de cone en croyant qu'il s'agit d'un tronc de sphere.
Pourquoi parlons-nous de ça ? Juste pour montrer qu'avoir une confiance aveugle dans les resultats donnés par un ordinateur sur la base de suppositions discutables peut conduire à des certitudes ne reflétant pas la réalité. Et plus l'algorithme est sophistiqué, plus il faut de precautions pour ne pas se tromper grossierement.
Prenons un exemple (très) caricatural. On veut réaliser un cylindre de révolution, mais on obtient une pièce à section légèrement elliptique. Si on mesure un seul diamètre, on en concluera qu'on a affaire à un cylindre de révolution parfait ce qui est inexact. Maintenant mesurons un foret en deux diamètres situés dans le même plan contenant l'axe de révolution. Une mesure est faite sur les listels une seconde mesure est faire dans les goujures. On va en déduire qu'on a affaire à un tronc de cône !
Je sais que c'est tellement caricatural que certains ne vont pas me prendre au sérieux. Mais hélas qui n'a jamais vu un tourneur réaliser un alésage sur 100 mm de profondeur, mesurer son diamètre d'entrée et le déclarer conforme d'un seul coup de pied à coulisse ou de micromètre ?
Je vois déjà venir des mécaniciens experimentés qui vont me dire : je connais ma machine, je sais qu'elle est capable de tenir la tolérance demandée. Je ne peux que m'incliner devant l'experience. Mais encore faut-il en avoir assez. Prenons l'exemple d'un alesage de bossages d'axe de piston moderne. L'immense majorité des mécaniciens croit qu'il est cylindrique. C'est une erreur. Dans les moteurs modernes, ces alesages ont des formes "en trompette" qui permettent d'absorber les flexions d'axes tout en reduisant le jeu. Soit on fait un montage à l'ancienne parfaiement cylindrique avec jeu consequent et le moteur sera bruyant au ralenti, soit on realise un montage moderne "à trompettes" avec jeu reduit. Mais un montage cylindrique parfait à la cote minimale d'un alesage de bossage de piston moderne finira dans la benne à ferraille, même si l'ajustement est jugé "parfaitement glissant juste" avant montage dans le moteur.
Pourquoi ?
Justement parce que l'hypothèse de cylindricité de départ était illicite.
Tolérances de localisation
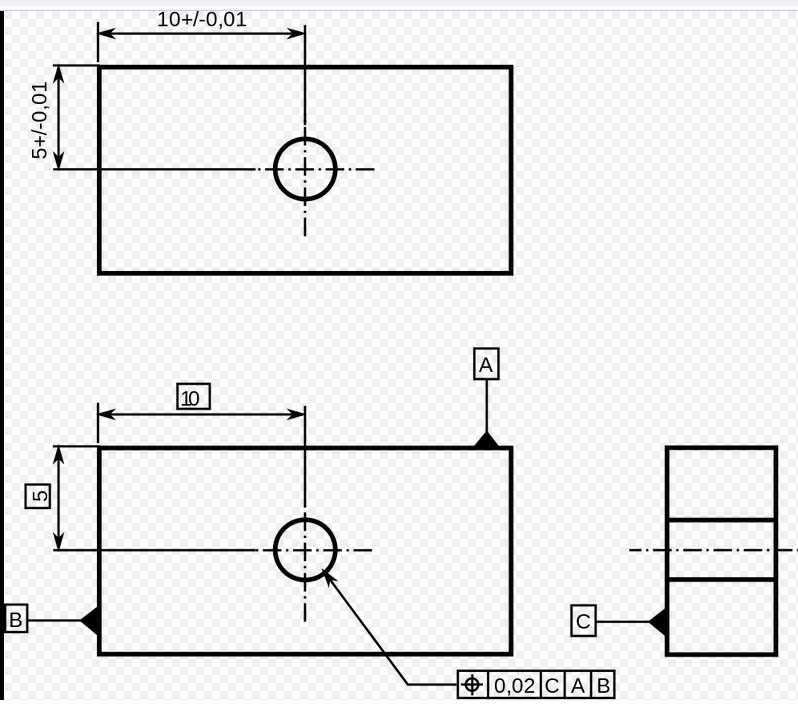
Admettons qu'on dispose d'un moyen de mesure parfait, et qu'on soit capables de modéliser de manière parfaite une surface parfaite. On veut réaliser un trou de goupille de telle manière que l'axe du trou ne dévie pas de plus de 0,02 mm par rapport à un angle de la pièce. Ci-dessous, deux méthodes de cotation QUI NE SONT PAS EQUIVALENTES.
Dans le premier cas, la zone de tolérance projetée sur la surface C est un carré de 0,02 mm de côté.
Dans le second cas, la zone de tolérance projetée sur la surface C est un cercle de 0,01 mm de rayon (donc de 0,02 mm de diamètre.)
Une pièce réalisée de telle manière que l'axe du trou soit juste dans un angle du carré de tolérance sera considérée comme bonne avec le premier plan et mauvaise avec le second.
Avec le premier plan la localisation de l'axe du trou pourrait varier de + ou- 0,014 mm alors qu'avec la seconde définition la variation autorisée n'est que de ou- 0,01 mm.
Si vous avez un doute, ne vous inquiétez pas si vous n'avez pas fait maths sup. Pensez au théorême de Pythagore : dans un triangle rectangle le carré de l'hypothénuse est égal à la somme des carrés des deux autres côtés. On apprenait ça à dix ans autrefois.
Demonstration :
Somme des carrés des deux cotés de la demi-zone de tolérance (0,01 x 0,01) + (0,01 x 0,01) = 0, 0002
Longueur de l'hypothénuse : Racine carrée de 0,0002 = 0,01414...
Tolérance de forme
La tolérance de forme indique l'écart maximal toléré entre la surface idéale définie par le plan et la surface réelle obtenue. Les limites de tolérances correspondent à des surfaces théoriques déportées de la surface idéale de la moitié de la largeur de la tolérance. Par exemple, une tolérance de planéité de 0,02 est délimitée par deux plans séparés par 0,02 mm. Tous les points de la surface réelle doivent être contenus entre les deux surfaces limites de tolérance.
Vidéo empruntée à la chaîne Youtube Hey m'sieur
Là encore, il n'y a pas équivalence entre une tolérance de forme et une cote tolérancée entre deux surfaces. La tolérance de forme limite l'écart de forme. la côte tolérancée limite l'écart de dimension. avec la côte tolérancée, une pièce "en banane" peut être acceptée si son épaisseur est constante alors qu'avec une tolérance de forme elle serait refusée si la surface est trop courbée.
Typiquement, ce cas se produit souvent un avec lardon de réglage de chariot rectifié. Si le lardon est courbe mais d'épaisseur constante, le chariot se bloquera alors qu'il coulisserait facilement si la forme de la surface était conforme.
les tolérances de forme courantes sont : rectitude, planéité, circularité, cylindricité, sphéricité, conicité.
Il est très important de bien comprendre la différence entre circularité et cylindricité. La circularité se mesure dans un plan, la circularité dans l'espace. Une "banane" peut être conforme en circularité mais pas en cylindricité. Concrètement une pièce longue circulaire, mais pas cylindrique se coincera peut-être dans un alésage ajusté.
Pour les autres tolérances de forme, je vous invite à consulter la chaine youtube citée en référence : https://www.youtube.com/@heymsieur2776
Pourquoi refaire ce qui est déjà très bien fait ?
Tolérance de position
La tolérance de position détermine la position (position vraie) de l'élément par rapport à une (ou plusieurs) références. La (les) références doit(vent) être spécifiée(s).
Les tolérances de position les plus courantes sont : parallélisme, perpendicularité, inclinaison, concentricité, coaxialité.
Là aussi, il est très important de bien maîtriser la différence entre concentricité et circularité. C'est à ce niveau que beaucoup d'amateurs (et même certains professionnels) se trompent.Pour faire simple disons que la coaxialité est en trois dimensions ce que la concentricité est en deux dimensions seulement.
Un tour équipé d'un mandrin quatre mors réalise assez facilement des surfaces concentriques pour peu qu'on sache le régler. Mais beaucoup plus difficilement des surfaces coaxiales.
Regardez bien les plaquettes commerciales des marchands d'outillages. Presque tout le monde vous parle de concentricité, dont on se moque la plupart du temps, et peu donnent des informations sur la coaxialité qui est pourtant un critère très important pour le fonctionnement de nombreux dispositifs.
Tolérances de rugosité
Ordres de grandeur
Une surface est définie de manière théorique sur un plan : c'est un plan, une sphère, un cône, etc.
Dans la réalité, la pièce comporte des défauts du premier ordre, ils sont normalement définis par les tolérances de position. Les défauts du second ordre (ondulations) sont limités par les tolérances de forme.
Les tolérances de rugosité définissent les limites d'acceptabilité des défauts du troisième et du quatrième ordre.
Caractérisation de la rugosité
Ci-dessous la coupe d'une surface fortement grossie. L'échelle des défauts n'est pas respectée. La rugosité se mesure en microns (micromètres.)
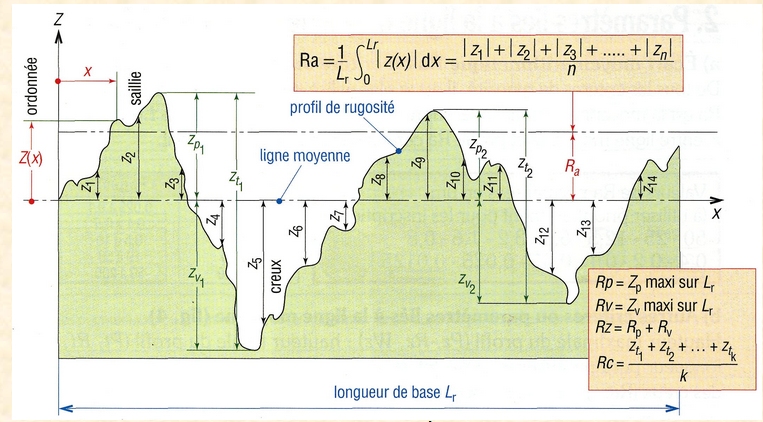
La ligne moyenne définit les ondulations de surface (défauts du second ordre.)
La distance entre deux pics principaux définit le Pas de rugosité. En usinage, généralement le pas de rugosité est défini par l'avance de l'outil. En rectification, il est souvent conditionné par l'équilibrage de la meule et l'avance de la pièce.
Le pas de rugosité est généralement observable à l'oeil nu. Il s'agit d'une observation souvent empirique qui donne quelques indications sur la qualité de la surface, mais qui ne suffit pas à la caractériser suffisamment. Néanmoins ce type d'observation est très utilisé par les mécaniciens. Par exemple, pour estimer (grossièrement) l'état de surface d'une chemise de moteur.
La rugosité peut être caractérisée de différentes manières.
Rt (rugosité totale)
Rt désigne la différence d'altitude entre le plus haut pic et le plus haut creux sur la surface contrôlée.
Rz (régularité)
Rz, désigne la valeur moyenne des cinq plus grandes valeurs de Rt trouvées sur la surface contrôlée.
Rt et Rz sont très fortement impactées par le rodage des pièces en fonctionnement.
Ra (rugosité arithmétique)
Ra désigne le résultat de la moyenne de l'intégration des différents écarts d'altitude par rapport à la ligne moyenne. ra est donc une valeur statistique qui ne donne aucune information sur les valeurs maximales des pics et des creux. Pa définition Ra ne peut jamais être supérieur à la moitié de Rz (puisqu'il s'agit d'un écart avec la moyenne.)
Ra est le paramètre le plus souvent spécifié par les concepteurs, mais il ne suffit pas pour caractériser une surface puisqu'il n'est qu'une moyenne. Pourrait-on habiller correctement une population de gens si on ne prenait en compte que la taille moyenne des individus ?
Contrairement à ce qu'on entend ou lit très souvent Ra par nature ne peut pas être observé à l'oeil. De plus Ra n'est pas suffisant pour caractériser une surface. Vous en doutez ? Allez-donc consulter la page que j'ai consacré à la fatigue mécanique. J'y fais la démonstration que cette façon de procéder est illusoire quand on a affaire à des applications pointues. C'est ici : La fatigue mécanique. Troisième partie : Comment améliorer la tenue en fatigue d'une pièce ?
Les comités de normalisation, conscients de l'insuffisance de cette définition ont prévu qu'on puisse spécifier plusieurs paramètres pour une seule surface, des paramètres géométriques mais aussi des paramètres concernant le procédé d'obtention, car la morphologie à l'échelle microscopique est très fortement conditionnée par le processus de fabrication. En 14 ans d'expertises de défaillances sur des moteurs fortement chargés, j'ai rencontré bon nombres d'avaries directement imputables soit à une définition insuffisamment restrictive soit insuffisamment respectée.
Plus d'informations sur la norme ISO 1302 sur le document mis en ligne par L'Institut National de Sciences Appliquées de Lyon. Lien
CONCLUSION ET PERSPECTIVES
Dans cette première partie, nous avons essayé de faire prendre conscience que la définition d'une pièce ne se borne pas à indiquer une cote tolérancée. Nous n'entrerons pas ici dans des méthodes de bureau d'études qui permettent de définir les besoins. Néanmoins nous espérons que la prise de conscience sera suffisante pour que ceux qui doivent réaliser ou contrôler des pièces soient convaincus que toutes les indications qui figurent sur un dessin de définition de pièce doivent être respectées afin de garantir la montabilité des pièces, leur performance en service et leur durabilité.
L'amélioration de la performance des assemblages mécaniques dépend pour une large part d'une meilleure définition des besoins, de leurs respect, de leur contrôle. Dans une le seconde partie Lien vers seconde partie nous allons présenter les principaux moyens de mesure de dimensions.
Merci de votre fidélité.
A découvrir aussi
- La peinture. troisième partie l'application des couches de finition
- Usinage à l'outil. Première partie : les matériaux des outils
- Acheter une machine d'occasion
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 132 autres membres