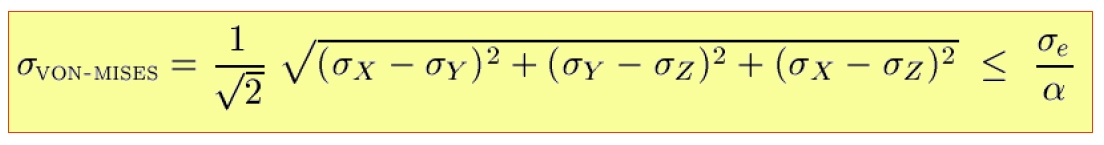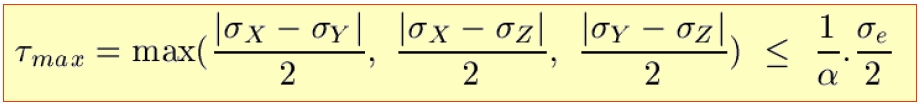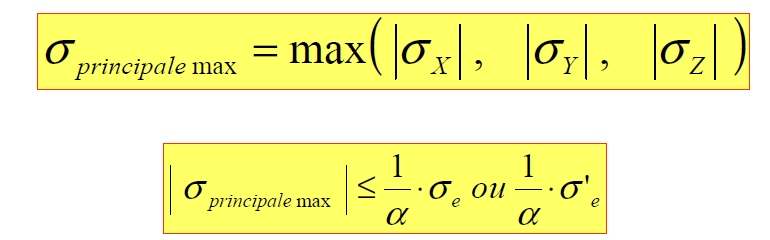THOMAS RACING DEVELOPPEMENT

INTRODUCTION

Dans la première partie de cet article, nous avons défini les modes de rupture des pièces mécaniques.

Nous avons expliqué comment une pièce bien dimensionnée pour résister à une sollicitation statique pouvait se rompre en fatigue après l'évolution d'une microfissure née au niveau d'un défaut, souvent microscopique, donc très difficilement décelable.

Dans cette seconde partie, nous allons présenter quelques méthodes de calcul qui permettent de prendre en compte le risque fatigue dans le dimensionnement. Mais avant d'entrer dans le vif du sujet, nous allons d'abord expliquer les bases du calcul de dimensionnement.

Cette partie est un peu abstraite et certains risquent d'avoir du mal à suivre jusqu'au bout. Qu'ils se rassurent, la troisième partie de cet article sera beaucoup plus pragmatique et facile à comprendre.

S'agissant du dimensionnement de pièces qui peuvent être critiques, nous rappelons aux lecteurs que les informations données ici le sont à titre d'information. Nous ne saurions être responsables en cas de coquille dans le texte ou d'erreur d'interprétation. Il convient de faire vérifier tout calcul de dimensionnement par un expert avant d'y accorder foi.

NOTIONS DE BASE DES CALCULS DE DIMMENSIONNEMENT

Rappel sur les contraintes

La contrainte moyenne à laquelle est soumise une section de pièce est égale à l'effort transmis par cette section divisé par sa surface.

Par exemple, lorsqu'on exerce une traction de  10 000 newtons sur une vis M8 x 125, la contrainte moyenne dans le corps de vis (partie non filetée) est égale à 10 000 / (4 x 4 x 3.14) = 199 newtons par millimètre carré.

Les mécaniciens ont l'habitude d'utiliser la lettre grecque sigma minuscule σ (signe en forme de sifflet d'agent de police) pour désigner les contraintes. Vous la retrouverez dans la majorité des formules.

Caractérisation des matériaux

La contrainte moyenne que peut supporter un matériau sans se déformer dépend de sa nature et de son état métallurgique (pour les métaux.) Par définition, la contrainte moyenne à laquelle s'allonge de manière irréversible un matériau dans un état métallurgique donné est appelée limite élastique par extension, en abrégé Re.  Plus d'infos en cliquant sur ce lien.

Pour chaque matériau, on trouve dans la littérature la valeur de Re pour les principaux états métallurgiques. Ces valeurs ont été déterminées expérimentalement.

Base du calcul en chargement statique

Connaissant l'effort et la section la plus faible qui doit résister à cet effort, il suffit de faire une division pour connaître la contrainte à laquelle elle sera soumise et choisir le matériau adapté.

Connaissant l'effort et la limite élastique du matériau, il suffit de faire une division pour dimensionner la section nécessaire pour que la pièce ne se déforme pas.

Coefficient de sécurité.

Les calculs précédents permettent de dimensionner la pièce pour qu'elle se situe à sa limite élastique sous l'effort maximal. Evidemment ce n'est généralement pas ce qu'on recherche. habituellement, on souhaite que la pièce ne se déforme jamais de manière irréversible. Pour cela, on applique un coefficient de sécurité afin de majorer la section soumise à l'effort.

Pour une pièce quelconque, le coefficient choisi est généralement 2.

Pour une pièce critique (pièce dont la rupture pourrait provoquer un accident, par exemple) on n'hésite pas à majorer ce coefficient.

Limites du principe

Dans tout ce qui précède, on a considéré uniquement la contrainte moyenne.  Cette méthode suppose donc que la contrainte soit uniformément répartie dans la section de la pièce. C'est rarement le cas. Par exemple, si on appliquait cette méthode à la vis M8 x 125 citée plus haut au niveau de la partie filetée, on aboutirait à une contrainte minorée parce que le filet concentre les contraintes. La section calculée dans la zone filetée est égale à la section dans la zone non filetée (4 x 4 x 3.14), moins la section du filet (3,14 x 8 x (1,25/2) * soit 34,54 mm² au lieu de 50,24 mm², ce qui donnerait une contrainte moyenne de 290 newtons par millimètre carré.

* En fait, les fabricants de vis utilisent une autre formule parce que le filet est oblique. il ne réduit donc la section que d'un côté de la vis

Or, la contrainte ne se répartit pas de manière homogène au niveau des filets. On le voit bien sur la simulation numérique que j'ai présentée dans les pages relatives aux filetages. 

lien vers filetages 4eme partie

On a donc expérimentalement (depuis longtemps) puis plus récemment (moins d'une centaine d'années) par calculs défini des coefficients de concentration de contrainte qu'on multiplie par le coefficient de sécurité pour définir un coefficient plus réaliste.

On trouve ces coefficients de concentration de contrainte dans la littérature. On les appelle Kt en France, Alpha dans certains pays étrangers.

Par exemple ici : Lien 1  (niveau débutant) , là  Lien 2 niveau intermédiaire ou là : Lien 3 (niveau ingénieur)

Les liens ci-dessus téléchargent un fichier pdf sur votre ordinateur.

Pour la vis qui nous sert de référence, les concentrations de contraintes sont particulièrement importantes dans la zone filetée.

Pour les assemblages statiques (donc hors fatigue) W THOMALA communique les coefficients suivants :

• dans le corps du boulon (partie non filetée) : 1 (correspond à notre premier calcul)
• Au niveau du premier filet (côté tête) : 3 à 4 (ceux qui ont de l'expérience auront remarqué que les vis cassent parfois ce niveau.)
• dans le filetage qui n'est pas en prise  (entre le corps et l'écrou) : 2 à 3
• Au niveau du premier filet en prise avec l'écrou : 10 (la majorité des ruptures de vis se produisent à cet endroit.)

Source : Centre Technique des Industries Mécaniques

Ici, la contrainte maximale au niveau du premier filet de la vis de 8 sur laquelle on exerce une traction de 10 000 newtons devrait avoisiner les 3000 newtons par millimètre carré. mais puisque cette contrainte est supérieure à la limite élastique, la matière va se déformer localement pour adopter une forme plus propice qui contribuera à minimiser la contrainte locale. Après ce conformage, la zone fortement contrainte sera plus grande, mais la contrainte maximale diminuera.

Cependant, cette diminution locale de contrainte n'est possible que si le matériau est suffisamment ductile. Une fois écroui, il n'aura plus la possibilité de s'adapter à nouveau. Or, les filets de vis sont obtenus par roulage, donc déjà fortement écrouis. par conséquent la faculté d'adaptation locale est assez faible.

Outils numériques

Les logiciels de simulation numérique donnent les contraintes locales. On peut donc s'affranchir du coefficient de concentration de contrainte s'ils ont été correctement paramétrés. Attention :  mon expérience, le paramétrage n'est pas aussi simple qu'il n'y parait. faire un calcul numérique correct est une affaire de spécialiste bien formé et avec de l'expérience. De trop nombreux jeunes ingénieurs inexpérimentés calculent tout et n'importe quoi.  Et même les bons professionnels ne sont jamais à l'abri d'une erreur. Il convient d'être extrêmement prudent avec les outils numériques, notamment parce qu'on ne connait pas toujours le contenu du code source.

Tous les logiciels que je connais considèrent la matière comme élastique. par conséquent, ils indiquent souvent de contraintes que la matière n'est pas capable de supporter. Ces contraintes n''existent en fait jamais. Soit la matière s'adapte localement et la contrainte diminue, soit la matière ne peut pas s'adapter et la pièce casse. Il n'y a donc plus de contrainte.

THEORIE DE LA FATIGUE

 Dans ce qui précède, nous avons vu les principaux critères à pendre en compte pour dimensionner de manière rationnelle une pièce soumise à un chargement statique. Il s'agit d'une approche macroscopique.

Dans la première partie de cet article, nous avions montré qu'elle ne suffit pas lorsque les pièces sont soumises à des sollicitions dynamiques. C'est le cas de la majorité des pièces de moteurs, de transmissions, de suspensions.  Un mécanicien qui travaille sur un véhicule, un bateau ou un avion ne peut pas ignorer les mécanismes qui conduisent aux ruptures en fatigue parce que le chargement des pièces sur lesquelles ils travaille n'est pas constant.

Ecrouissage et fatigue

Avant d'aller plus loin, il importe de bien distinguer rupture après écrouissage et rupture en fatigue. Lorsqu'on plie un barreau d'acier au-delà de sa limite élastique on écrouit le métal (voir courbe d'allongement lien.)

Le métal écroui perd sa faculté d'allongement. Par conséquent si on essaye de redresser une pièce pliée et écrouie, elle doit s'allonger dans le sens opposé ce qui n'est possible qu'avec une augmentation de la contrainte locale conduisant à encore plus d'écrouissage. Après quelques pliages et redressages, la contrainte dépasse la limite à la rupture et la pièce se rompt. mais il ne s'agit pas de fatigue. L'observation de la zone de fracture le montre bien.

Au contraire, en fatigue la contrainte ne dépasse généralement pas la limite élastique au cours de la vie de la pièce. Elle n'est atteinte et dépassée que lors de la rupture finale. En fatigue conventionnelle, il n'y a pas d'écrouissage du matériau à l'échelle macroscopique.

Différents types de fatigue

La fatigue conventionnelle est un processus de fatigue pure, telle que nous l'avons décrite dans la première partie de cet article. Les auteurs s'accordent généralement pour considérer qu'on a affaire à de la fatigue conventionnelle  à partir de 50 000 cycles de sollicitation.

La fatigue oligocyclique est un processus plus complexe puisque s'y mèlent l'écrouissage et une part de fatigue. L'étude de la fatigue oligocyclique sort du cadre de cet article.

Courbes de Wohler

Les courbes de Wohler sont le plus ancien outil servant à pré-déterminer la tenue en fatigue des pièces. partant du principe qu'une pièce calculée en statique va se briser rapidement en fatigue et qu'une pièce fortement surdimensionnée ne se brisera jamais, Wohler a essayé de déterminer la durée de vie prévisionnelle des pièces en fonction de la contrainte qu'elles subissent.

Wohler a étudié de manière statistique le comportement des pièces. Les courbes qu'il en a tiré représentent la probabilité de rupture. les plus courantes sont établies à 50 % de chance de défaillance. Le nombre de cycles est en abscisse avec une échelle logarithmique. La contrainte est reportée en ordonnée avec soit une échelle linéaire, soit une échelle logarithmique.

Une courbe de Wohler représente donc la synthèse de nombreux essais. Dans l'immense majorité des cas, les essais se font en flexion rotative.  Une machine de flexion rotative s'apparente à un tour de mécanicien. La pièce est entrainée par un mandrin et son extrémité est tenue par une lunette volontairement excentrée. A chaque tour la pièce est contrainte de flechir alternativement dans un sens puis dans l'autre.

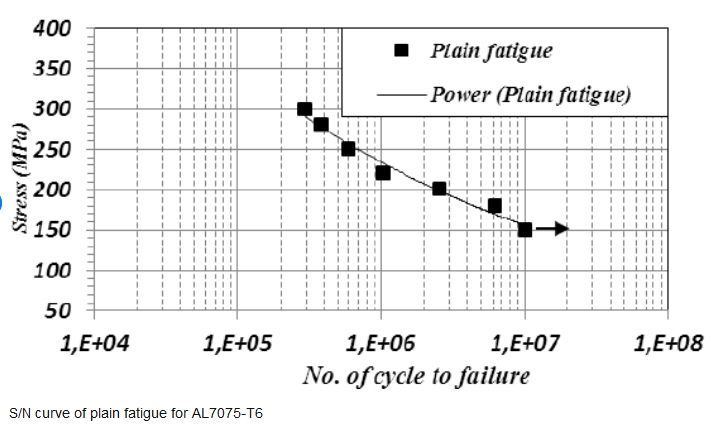
On obtient des courbes, telles que celle-ci (alliage 7075 T6)

 Toutes les courbes de Wohler se terminent par une asymptote. Il est convenu de considérer qu'en-deça de la contrainte qui permet d'atteindre 10 millions de cycles la durée de vie est infinie. 10 millions de cycles peuvent paraître beaucoup. Dans un moteur qui tourne à 6000 tours par minute, la bielle subit 100 cycles par seconde. 10 millions de cycles sont atteints en une trentaine d'heures de fonctionnement.

Les courbes de Wohler sont une base de travail. Cependant, en fonction de la criticité de la pièce, il faut être très prudent en les utilisant. D'une part, il faut connaître le taux de défaillance. Une courbe à 50 % signifie que 50 % des pièces ont cassé sur le point de chargement considéré. Il faut aussi tenir compte des conditions réelles d'utilisation du matériau. Par exemple ici le 7075 perd environ la moitié de sa résistance mécanique à 200 °C.

Il faut enfin bien considérer la façon dont les éprouvettes sont sollicitées et comment elles sont réalisées. Une éprouvette de flexion rotative est une pièce qui ne comporte pas de singularité (Kt = 1.) Ce n'est pas toujours le cas des pièces réelles. Une éprouvette de flexion rotative est très finement polie. C'est très rarement le cas des pièces réelles. Ce n'est pas parce que le matériau et l'état métallurgique d'une éprouvette correspondent à celui de la pièce que les résultats sont transposables sans précaution. La propreté inclusionnaire de l'alliage est un paramètre impactant les résultats au premier ordre. C'est d'ailleurs pour cette raison que j'insiste tant sur ce blog sur ce point. la direction dans laquelle sont pris les échantillons intervient aussi. J'ai récupéré il y a quelques années des documents déclassifiés de l'armée américaine. Ils concernent des alliages aéronautiques et des superalliages. Les différences entre direction de laminage et direction transverse sont très importantes.

Lassé de subir des déconvenues, j'avais invité le commercial d'Aubert et Duval qui me fournissait à une réunion pour tenter de comprendre pourquoi les matériaux d'exception qu'il me vendait ne donnaient pas toujours les résultats escomptés (bien qu'ils soient généralement nettement meilleurs que ceux des concurrents.) Notre discussion a été fructueuse. J'ai compris grâce à lui qu'on ne peut accorder foi à ce type de courbes (et aux autres outils que je vais présenter) que si tous les paramètres sont équivalents entre le test et les conditions de fonctionnement réelles. 

La conclusion de notre entretien est que la hiérarchie des matériaux testés tous dans des conditions identiques par l'aciériste est représentative de celle de ces matériaux dans les pièces réelles, mais qu'il n'existe pas de moyen de déterminer la tenue en fatigue d'une pièce à-partir de courbes standard qui ne tiennent pas compte des spécificités de cette pièce.

Alors, me direz-vous pourquoi ne pas tester sur les pièces plutôt que sur éprouvettes ?

D'abord casser des éprouvettes coûte nettement moins cher que de casser des moteurs. Et les résultats sont plus rapidement exploitables. De plus, il existe des méthodes pour casser plus rapidement les éprouvettes et gagner ainsi un temps considérable. Les essais Staircase et  Locati en sont de beaux exemples.

Voir par exemple Thèse de Pauline  BEAUMONT (Université d’Angers, 2013)

Finalement, cela conduit a réaliser soi-même les essais pour obtenir des courbes de Wohler plus représentatives des conditions réelles de fonctionnement.

Un autre problème de la flexion rotative ordinaire est que la contrainte moyenne est nulle et la contrainte alternée parfaitement symétrique (loi sinusoidale de moyenne nulle.) Ce n'est pas toujours le cas pour le chargement des pièces. Une bielle, par exemple, subit une sollicitation qui n'est pas de flexion avec une loi de chargement  qui n'est pas strictement sinusoidale.

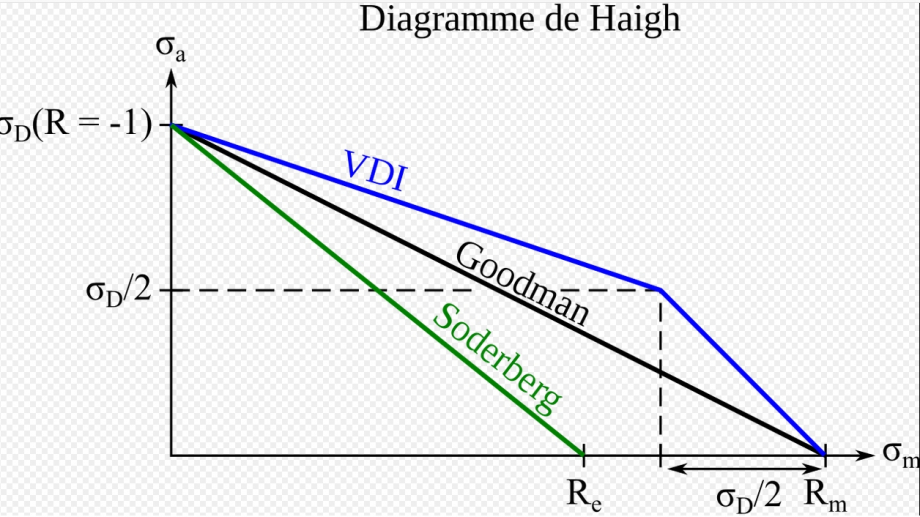
Diagramme de Haigh

Le diagramme de Haigh est un outil qui permet de prendre en compte l'état moyen de traction sous sollicitation uniaxiale.

Cas typique : pièce chargée en permanence et soumise en plus à une sollicitation cyclique dans la direction de la charge Autrement formulé, c'est de la fatigue simple avec précontrainte dirigée de la même manière que la charge cyclique. Exemple : une vis de tete de bielle serrée (donc tendue) qui subit une charge variable suivant l'angle pris par le vilebrequin.

Sur le diagramme de Haigh, on trace les contraintes Re et Rm du matériau en abscisses et la limite d'endurance (contrainte admissible à dix millions de cycles) en ordonnée.

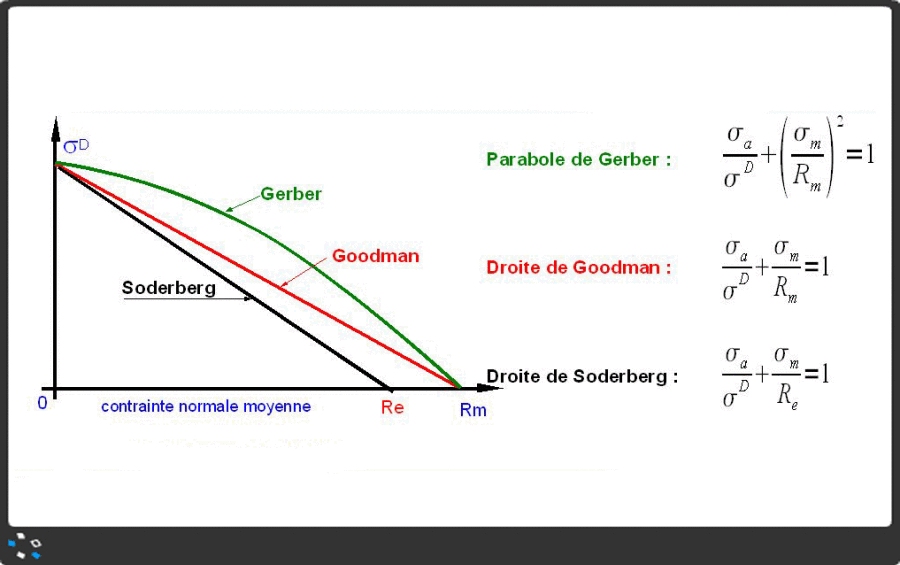
Une fois ces points tracés on peut tracer la droite de  Goodman, celle de Soderberg ou la courbe parabolique de Gerber.

Si on ne veut pas tracer la parabole, on peut la réprésenter par deux demies-droites.

En fonction de la criticité, chaque métier a sa courbe préférée : l'automobile travaille de préférence avec la courbe de Gerber, l'avionique préfère celle de Goodman, enfin pour les applications les plus critiques celle de Soderberg est celle qui apporte la sécurité maximale.

La courbe choisie constitue la limite à ne pas franchir pour garantir la tenue en fatigue de la pièce.  On place sur le graphique le point correspondant en abscisse à la contrainte permanente et en ordonnée à la contrainte alternée. Si le point se situe sous la courbe de référence, le fonctionnement est validé, si le point se situe au-dessus, le fonctionnement en fatigue est non validé.

Diagramme de ROSS

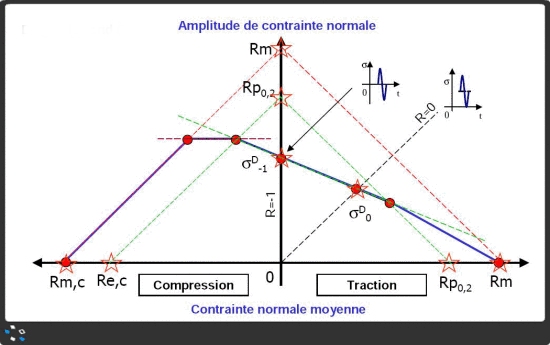
Le diagramme de Haigh ne prend pas en compte le sens de la sollicitation constante. Autrement formulé, il est utilisable que la précontrainte soit de compression ou de traction. Cependant, cette approche est excessivement sécuritaire quand la contrainte constante est une contrainte de compression. Le diagramme de ROSS corrige ce handicap.

Document Ecole des Mines de Douai

On l'utilise de la même manière que le diagramme de Haigh, mais le sens de la précontrainte est pris en compte. Pour le construire, on place les points Re et Rm de compression symétriques de Re et Rm par rapport à l'axe des ordonnées du diagramme de Haigh et on prolonge la courbe de Gerber simplifiée jusqu'au point où elle coupe une droite issue de Re compression et passant par Re sur l'axe des ordonnées. Si le repère est orthonormé, cette droite a une pente de 45 °. A partir de ce point la courbe de Gerber simplifiée est prolongée horizontalement jusqu'à ce qu'elle coupe une droite issue de Rm Compression passant par Rm projeté sur l'axe des ordonnées. cette droite est parallèle à celle qui joint les points Re. Ensuite, la courbe de Gerber simplifiée suit la courbe de Rm compression.

Comment calculer si la sollicitation n'est pas uniaxiale ?

Il arrive très souvent qu'une pièce soit sujette à des sollicitations complexes. En mécanique statique, on utilise couramment le critère de Von Mises pour calculer la résistance des pièces. Le critère de Von Mises associe une contrainte équivalente à l'ensemble des contraintes auxquelles est soumise la pièce.

La contrainte de Von Mises dépend de la racine carrée d'une somme de carrés de différences de contraintes.

Le calcul de cette contrainte équivalente commence à être compliqué pour un amateur.

Le critère de Tresca, quoique beaucoup moins employé est un peu plus facile à calculer

Ne  prenez pas trop vite vos jambes à votre cou. Pour des sollicitations simples, la majorité des termes de l'équation sont nuls. Elle n'est donc pas aussi compliquée à calculer qu'il n'y parait au premier abord.

Tresca et Von Mises ne sont applicables que si la pièce est dans un matériau ductile parce qu'elle va se déformer pour s'adapter aux excès de contraintes. Dans le cas d'une pièce fragile, c'est-à dire inapte aux déformations ductiles, on utilise le critère de Rankine.

Par conséquent, pour une sollicitation composée statique et sur une pièce ne présentant pas de singularité (sans concentration de contrainte), le calcul reste encore gérable avec des moyens rudimentaires.

ça se complique un peu si la pièce présente des singularités puisqu'il va falloir tenir compte des coefficients de concentration de contrainte. A ce niveau, l'aide d'un ordinateur est appréciable.

Mais à partir du moment ou en plus de la sollicitation statique, une ou des contraintes alternées viennent affecter la pièce, le calcul devient une affaire de spécialiste disposant de logiciels adaptés. Il n'est pas en mon pouvoir de vous en inculquer ne serait-ce que les rudiments. Même si j'en ai entendu parler, je n'ai pas suffisamment de maîtrise du sujet pour cela. Plusieurs méthodes de calcul reposent sur le postulat que la matière sollicitée peut subir des plastifications locales qui vont contribuer à minimiser la contrainte de Von Mises locale. Certaines s'intéressent à l'échelle mésoscopique, alors que d'autres ont une vision plus globale. Les méthodes les plus récentes sont basées sur une approche énergétique.

Néanmoins j'invite les plus curieux à faire quelques recherches sur les sujets suivants :

Critère de Crosland (basé sur l'approche Von Mises, 1956)

Critère de Matake (basé sur une approche macroscopique, 1980)

Critère de Dang Van (basé sur une approche macro-mésoscopique , le matériau reste globalement élastique, mais subit des plastifications à l'échelle atomique, 1973)

Critère de Papadopoulos (Dang Van amélioré en 1993)

Critère énergétique du LAMEFIP ou autres

Ce dernier paragraphe pour prendre conscience que les mécanismes modernes sont conçus avec des connaissances et des moyens techniques dont l'amateur ne dispose généralement pas.

Vouloir faire mieux qu'une pièce de série en termes de résistance des matériaux est un sacré challenge. Nous verrons dans la troisième partie de cet article que le mécanicien amateur à encore la possibilité d'améliorer la tenue en fatigue des pièces de série avec des moyens somme toutes assez conventionnels. Quant à concevoir des pièces de moteur de Formule un dans son garage, c'est du passé. On peut le regretter, mais tous les pilotes le savent bien, celui qui finit toujours par gagner, c'est le temps. On ne l'arrête jamais...

Lien vers la troisième partie