Filetage quatrième partie : étude des assemblages vissés, théories de serrage et de résistance des matériaux appliquées

Dans la première partie de cet article, les différents types de filetages triangulaires courants ont été présentés. Lien vers la première partie

La seconde partie a abordé les problématiques de réalisation des taraudages (filetages femelle) et les outillages utilisés en fabrication ou en réparation. Lien vers la seconde partie

La troisième partie est consacrée à la réalisation des filetages mâles. Lien vers la troisième partie

Cette quatrième partie va s'intéresser aux problématiques de bureau d'étude :

- classes de qualité de visserie (aspect matériaux)

- dimensionnement des assemblages filetés statiques

- méthodes de serrage

- notions de dimensionnement des assemblages filetés soumis à des sollicitations dynamiques

- présentation de quelques résultats de calculs numériques et de ce que l'amateur peut en retenir quand il conçoit des assemblages filetés.

Cette partie est de très loin la plus compliquée à saisir. Sa compréhension peut demander quelques efforts à ceux qui ont un peu de mal avec la physique et l'approche scientifique. Qu'ils ne se découragent pas à la première lecture car c'est de très loin la plus intéressante à connaitre. Grâce aux renseignements communiqués ici, un amateur pourra rivaliser avec la plupart des bureaux d'études généralistes. Les assemblages qu'il concevra et réalisera seront fiables. C'est la première qualité qu'on demande à une voiture de course. Il est cependant demandé expressément à nos lecteurs de faire vérifier systématiquement leurs calculs avant de se lancer dans la réalisation de montages sur la base de ces calculs. En cas d'accident, nous ne saurions être tenus pour responsables, ni des erreurs qui auraient pu se glisser dans ce texte, ni de celles qui pourraient être faites par ailleurs.

Pour appliquer ce qui suit, il est nécessaire de savoir calculer une règle de trois. Les notions auxquelles il est fait référence étaient enseignées aux élèves de seconde de l'enseignement technique. Mais ça c'était avant. Avant qu'à grands coups de réformes, nos hommes politiques permettent à des étudiants d'obtenir des diplômes BAC + 5 en ne sachant même pas écrire un paragraphe sans faire au moins une faute par ligne ou soient totalement incapables de faire une multiplication à deux chiffres sans l'aide d'une calculatrice à huit chiffres... Pauvre France 2.0 dégénérée...

Avant de lire cette quatrième partie, il est conseillé de lire les trois parties précédentes bien que les problématiques abordées soient relativement décorrélées.

Préambule

La plupart des néophytes ont tendance à modéliser un assemblage vissé comme une boutonnière de chemise. Une fois en place, le bouton maintient les pièces de tissu immobiles et tant que le bouton est en place, il n'existe de possibilité de mouvement que si le fil qui maintient le bouton cède. Ce modèle correspond donc à une liaison par obstacle infiniment rigide.

L'approche qui est la notre et qui est partagée par tous les experts des assemblages filetés est très différente. Dans cette approche, la vis est considérée comme un ressort qui plaque les pièces l'une sur l'autre et par conséquent, c'est le frottement des pièces qui empêche leurs déplacements relatifs. La vis ne travaille donc pas au cisaillement, mais en traction. La plupart des assemblages filetés sont conçus de cette manière. C'est la conception que nous recommandons pour le cas général. Tout ce qui suit immédiatement ne concerne que les assemblages de ce type.

Mais parfois, on est contraint de faire travailler des vis au cisaillement. Dans ce cas on devra impérativement ne cisailler que le corps de vis, jamais le filetage qui n'est pas conçu pour ça. Les cas des vis qui travaillent cisaillement sera abordé plus bas.

On pourrait aussi imaginer de solliciter les vis en flexion. Ce type de montage est à proscrire absolument. Une vis n'est pas faite pour travailler ainsi. Le risque de rupture ou de desserrage est bien trop important pour qu'on s'y risque.

Rappel : notion de contrainte

En résistance des matériaux, on appelle contrainte moyenne la valeur d'un effort auquel est soumise une pièce divisée par la section de la pièce soumise à l'effort. C'est donc une force divisée par une surface. La contrainte a donc la même dimension qu'une pression.

Il existe des contraintes de compression, parfaitement comparables aux pressions, des contraintes de traction (effet inverse de la compression), des contraintes de torsion, des contraintes de cisaillement, des contraintes de flexion. Les contraintes de cisaillement, de torsion, de flexion et soit de traction soit de compression peuvent être appliquées ensemble en certains points de la matière des pièces. Toutes les contraintes peuvent être représentées par la composition de contraintes de traction et de compression. par exemple, dans une pièce cisaillée, une partie de la pièce est comprimée pendant que l'autre partie est en traction. Dans la majorité des cas, les contraintes de traction sont plus dangereuses que les contraintes de compression parce que la compression rapproche la matière alors que la traction la "déchire".

Rappel : comportement des matériaux métalliques sous sollicitation de traction

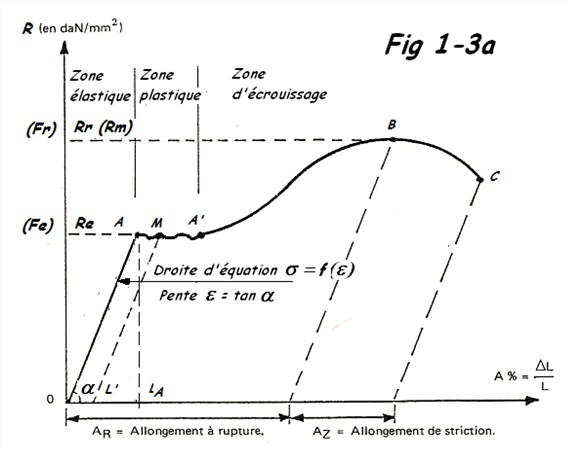
Pour bien comprendre tout ce qui suit, il est important de connaître le comportement des matériaux métalliques lorsqu'on les soumet à une sollicitation de traction. Voir la courbe ci-dessous qui illustre le texte suivant.

Lorsqu'on exerce une traction croissante sur une pièce métallique, elle commence par s'allonger de manière élastique. Tant que la contrainte de traction n'atteint pas une certaine valeur, le phénomène reste réversible. Si la sollicitation est supprimée, la pièce reprend ses dimensions initiales. Ce domaine de travail est appelé domaine élastique. Dans le domaine élastique, l'allongement de la pièce est parfaitement proportionnel à la contrainte exercée. C'est le domaine de travail normal des ressorts. Il s'étend jusqu'au point A de la courbe ci-dessous.

Si la contrainte exercée augmente au-delà de celle qui délimite le domaine élastique, la pièce continue de s'allonger, mais lorsque la contrainte est supprimée, la pièce ne reprend pas ses dimensions initiales. une partie de l'allongement persiste. La pièce a été étirée. On dit qu'elle est passée dans le domaine plastique.

La valeur de la contrainte qui correspond au passage du domaine élastique au domaine plastique est appelée limite élastique du matériau considéré. En abrégé on appelle la limite élastique Re (anciennement résistance élastique.)

Une fois dans le domaine plastique, l'allongement se poursuit tant qu'une contrainte de traction suffisante est maintenue, mais sans qu'il soit nécessaire qu'elle augmente. L''allongement plastique n'est donc pas proportionnel à la contrainte. A la fin du domaine plastique (point A' sur la courbe), commence un autre domaine appelé domaine d'écrouissage. La matière sollicitée sous fortes contraintes commence d'abord à augmenter sa résistance à l'effort. Pour l'allonger encore il faut que la contrainte augmente à nouveau .

Plus la pièce s'allonge dans le domaine d'écrouissage, plus sa section se réduit. On dit qu'une striction affecte la pièce. Cette striction conduit à une perte de résistance de la part de la pièce et elle continue de s'allonger alors même que la contrainte exercée diminue spontanément puisqu la pièce oppose de moins en moins de résistance à son allongement (entre les points B et C sur la courbe.)

A un moment, la striction devient telle que la pièce se rompt (point C de la courbe.)

On appelle limite à la rupture par extension la contrainte maximale qu' à pu supporter la pièce (mesurée au point B de la courbe. ) En abrégé, la limite à la rupture est appelée Rm (Anciennement résistance mécanique)

La graphique ci-dessous montre les tendances des matériaux métalliques.

Par convention (et pour des raisons de praticité lors de la caractérisation des matériaux) on a l'habitude de donner la valeur de Re avec 0,2 % d'allongement plastique (ce qui correspond au point M de la courbe. ) L'expérience montre que cette approximation est parfaitement acceptable pour les calculs. C'est pour cette raison que les fiches techniques des matériaux indiquent généralement les valeurs de Re0,2 et de Rm.

Pour les matériaux métalliques courants (aciers, alliages d'aluminium ou de cuivre, etc) les traitements thermiques et les modes d'obtention et de mise en forme du matériau affectent souvent très fortement les valeurs de Re0,2 et Rm. On ne peut donc rien calculer sans connaître précisément l'état métallurgique du matériau étudié (trempé, revenu, recuit, écroui, etc.)

Bases de la méthode de calcul de résistance des matériaux

Compte tenu de ce qui a été dit précédemment, on comprend que connaissant la sollicitation et les caractéristiques du matériau, on peut par calcul déterminer la section nécessaire pour que la pièce reste dans le domaine élastique.

Classes de résistance de la visserie du commerce

Visserie ISO (International Standard Organization)

Vis

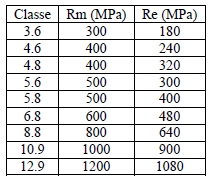
Les normes ISO définissent des classes de résistance des vis grâce à deux chiffres séparés par un point. Pour la visserie à haute résistance, ces chiffres et le point qui les sépare sont gravés dans les têtes de boulons.

Le premier chiffre indique la limite à la rupture par extension du matériau qui compose la vis. Il faut multiplier par 100 la valeur indiquée pour trouver cette limite à la rupture exprimée en MPa. par exemple une vis 8.8 a une limite à la rupture par extension de 800 MPa, soit 800 Newtons par millimètre carré. Ainsi, une vis M6 x100 qui a un noyau de 5 mm de diamètre (diamètre de la vis moins pas de la vis) a une section minimale de 2,5 x 2,5 x pi soit environ 19,5 mm². Elle est donc garantie pour résister au minimum à 19,5 x 800 = 15 700 Newtons. Elle peut donc supporter une masse de 15700 /9 ,81 = 1600 kg sans se rompre. (L'accélération de la pesanteur sur terre est égale à 9,81m/s², c'est à dire qu'un kilo de matière pèse 9,81 Newtons)

Le second chiffre, multiplié par le premier et multiplié par 10 indique la limite élastique du matériau de la vis. dans le cas de la vis M6 8.8, la limite élastique est égale à 8 x 8 x 10 = 640 Mpa et la vis peut supporter un poids de 19,5 x 640 = 12 480 Newtons (1272 Kg) sans s'allonger de façon permanente.

Les classes de visserie à haute résistance usuelles sont 8.8 ; 10.9 ; 12.9. Exceptionnellement et sur commande, on peut trouver de la 14.9. Certains matériaux (supéralliages) utilisés en aéronautique, aérospatiale, Formule un, etc. sont capables de meilleures performances, mais quasiment inaccessibles à l'amateur; Surtout parce que leur mise en oeuvre est très compliquée. Les vis de moindre qualité peuvent être réalisées en classe 3.6. Leur limite élastique est donc (12 x 9) / (3 x 6) = 6 fois plus faible que celle des vis 12.9.

Toute vis d'origine inconnue dont la tête ne porte aucun repérage (et c'est souvent le cas des productions de moindre qualité) doit être supposée de la plus faible qualité possible, soit Re = 180 MPa et Rm = 300 MPa.

Ecrous

Dans le système ISO, les écrous sont repérés par un seul chiffre. Un écrou de classe 8 est conçu pour ne jamais céder avant une vis de limite à la rupture de même classe soit 800 Mpa dans le cas présent.

On trouve facilement dans le commerce des écrous de classe 8 ou 10 et évidemment beaucoup d'écrous de classes inférieures. Les écrous de classe 8 ou 10 sont généralement repérés par un marquage, comme les vis à haute résistance.

Visserie impériale

ATTENTION AUX CLASSES DE RESISTANCE DES VIS IMPERIALES

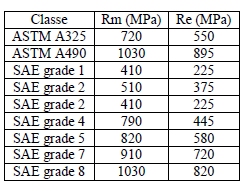
Le système de classes de résistance des vis impériales quoique différent du système ISO est comparable dans son esprit. Mais les valeurs gravées dans la visserie ne permettent de connaître les résistances que si on dispose du tableau suivant :

Au passage, on notera que l'équivalent de notre classe 12.9 n'apparaît pas dans ce tableau

Il faut se méfier des vis impériales qu'on remplace par des vis ISO. Une vis grade 8 ne peut pas être remplacée par une ISO 8.8, il faut au minimum une 10.9 !

Méthode de dimensionnement d'une vis

Traditionnellement, on a serré les vis dans le domaine élastique. Dans cette approche, La valeur de contrainte admissible est généralement forfaitairement fixée à 80 % de la limite élastique. Cette méthode, quoique très employée dans le domaine industriel, tend aujourd'hui a tomber en obsolescence chez les constructeurs automobiles, notamment parce que les logiciels de calcul par éléments finis permettent d'affiner fortement les hypothèses de calcul, mais aussi parce que les méthodes modernes de serrage offrent des avantages indéniables en termes de fiabilité et de réduction des coûts. Ces avantages s'ils sont certains, ne peuvent être obtenus qu'avec des moyens et une rigueur qui ne sont pas à la portée de l'immense majorité des amateurs de mécanique, ni même des meilleurs garagistes. Par conséquent dans ce qui suit, on se bornera à respecter l'état antérieur de l'art pour éliminer tout risque de malfaçon.

Principe de calcul

Le principe de calcul exposé ci-après n'est applicable que pour des matériaux au comportement purement élastique. par conséquent, la méthode n'est donc pas utilisable lorsque les éléments constitutifs de l'assemblage peuvent être sujets au fluage.

Fluage

Le comportement des matériaux présenté ci-dessus est celui d'une matière qui n'est pas sujette au fluage. Ces matériaux ont la propriété de conserver leur comportement élastique tant que la limite d'élasticité n'est pas atteinte quelle que soit la durée de la sollicitation. Une fois la contrainte éliminée, la pièce reprend ses dimensions initiales quelle que soit la durée pendant laquelle la contrainte a été appliquée. Ceci est vrai aussi bien en traction qu'en compression. Les matériaux soumis au fluage ont un comportement différent : lorsqu'une contrainte est appliquée pendant un certain temps, la matière se déforme de manière irréversible et d'autant plus que la contrainte est maintenue longtemps. A l'échelle microscopique, il y a donc un écoulement, plus ou moins lent de la matière.

Toutes les polymères thermoplastiques sont sujets plus ou moins au fluage. Tous les matériaux métalliques le sont également lorsqu'ils sont portés à des températures élevées. Au-delà de 700 °C, on doit s'inquiéter du fluage des aciers.

Loi de Hooke

La loi de Hooke définit le comportement des pièces élastiques. Elle n'est donc applicable que dans le domaine élastique.

F = k x l avec F = effort exercé, k = raideur de la pièce sous contrainte et l = allongement de la pièce [1]

On en déduit la raideur de la pièce k = l / F [2]

A savoir : les aciers, les alliages d'aluminium, les alliages de cuivre ont des propriétés mécaniques isotropiques. Cela signifie que la loi de Hooke est applicable aussi bien en traction qu'en compression. La valeur de K est identique en traction et en compression.

Module d'élasticité ou Module de Young

Chaque matériau au comportement purement élastique est définit par son module d'élasticité. il correspond à l'allongement relatif du matériau divisé par la contrainte subie par le matériau.

E = C x e, avec E = module d'élasticité, C = contrainte (= force / surface), e = allongement relatif = allongement / longueur initiale [3]

Attention : cette formule n'est applicable que dans le domaine élastique.

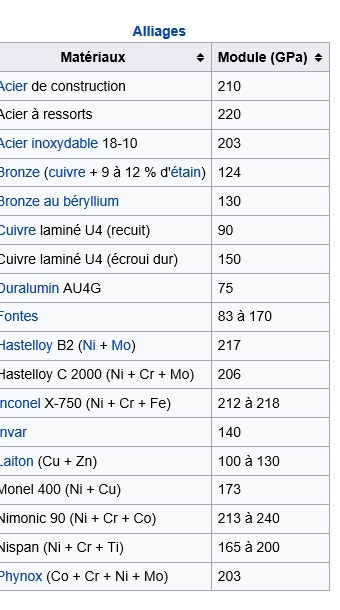
Le tableau ci dessous donne les modules de Young des principaux matériaux utilisés en mécanique.

Attention ces modules ne sont exacts qu' à 20 °C. Pour les aciers, ils sont utilisables avec une faible marge d'erreur jusqu'à 250 °C. Pour les alliages d'aluminium travaillant vers 200 °C, il faut les diviser par 2.

Hypothèses de départ

Puisqu'on se place dans une hypothèse de comportement purement élastique, l'allongement de la vis est proportionnel à l'effort que la vis exerce sur les pièces. La vis se comporte donc comme un ressort de traction.

L'écrou étant lui-même supposé purement élastique, il se comporte comme un ressort de compression.

Les pièces étant supposées comme purement élastiques, elles se comportent également comme des ressorts.

Pour que la vis ne se desserre pas avec les vibrations, il faut que sa tension reste toujours suffisante pour que des efforts soient appliqués aux points suivants :

- sous la tête de la vis ;

- entre le filet de la vis et celui de l'écrou (ou celui du taraudage) ;

- sous l'écrou s'il y a un écrou

- sur toutes les rondelles quand il y en a.

Comme il existe un coefficient de frottement entre les pièces et les éléments de visserie, il ne peut pas y avoir desserrage spontané tant que ces efforts sont présents. Le desserrage est d'autant plus difficile que la vis est tendue. On a donc intérêt à la serrer en créant le maximum de tension mais en restant dans la zone de fonctionnement élastique de la vis. Ainsi, si pour une raison quelconque il se produit un tassement de l'assemblage plus faible que l'allongement de la vis, il persistera un effort qui empêchera le desserrage.

Cas le plus simple : dimensionner une vis pour qu'elle ne se rompe pas sous l'effet d'une traction

On s'intéresse ici à une vis qui ne travaille pas en fatigue. C'est-à-dire dont le chargement n'évolue pas au fil du temps ou que le nombre de cycles d'évolution reste faible.

Si on utilise une vis normalisée à pas gros, avec un écrou normalisé de hauteur normale ou un taraudage dont la longueur est égale à au moins une fois le diamètre de la vis dans les métaux durs et 1,5 fois le diamètre dans les alliages légers, la section la plus critique est toujours celle qui se trouve au niveau du fond de filet. On verra plus bas qu'en cas de rupture, elle se produirait normalement au niveau du premier fond de filet en prise dans le taraudage.

Pour connaître la contrainte moyenne dans le noyau de la vis, il suffit de diviser l'effort de traction par la section du noyau de la vis

[(diamètre de la vis - pas de la vis) /2] x [(diamètre de la vis - pas de la vis) /2] x 3,14 [4]

. Cette contrainte doit toujours être inférieure à la limite élastique, sinon la vis pourra se desserrer.Dans la pratique, on évite de dépasser 80 % de la limite élastique.

Nota : la formule qui permet de calculer le noyau de la vis donnée ci-dessus n'est pas exactement celle qu'utilisent les fabricants de vis. Eux, utilisent une section légèrement supérieure car pour une vis à un seul filet (une vis courante, donc) il ne peut pas y avoir deux fonds de filet dans la même section perpendiculaire à l'axe de la pièce. La formule que nous communiquons convient très bien à l'amateur (et à de nombreux professionnels) car elle minimise les risques de rupture en minorant la section qui travaille réellement. Bien que ce point n'intéresse pas vraiment l'amateur, nous l'avons précisé parce qu'en absence de sa connaissance, la lecture des catalogues de fabricants de visserie pourrait désorienter les lecteurs.

Déterminer l'effort exercé en fonction du nombre de tours de serrage par une vis sur un assemblage supposé infiniment rigide

Domaine d'application : vis de dimensions significativement moindres que les objets sur lesquels elle exerce un effort et modules d'élasticité comparables.

Une fois les pièces plaquées, chaque fois que la vis fait un tour, elle s'allonge de la valeur du pas (on suppose ici que les filets ne sont pas déformés.)

L'effort exercé est égal à l'allongement absolu de la vis multiplié par la raideur de la vis.

La raideur de la vis est égale à la section de la vis multipliée par le module d'élasticité de son matériau. [5]

Par conséquent, l'effort exercé par la vis est égal au nombre de tours de vis, multiplié par le pas de la vis, multiplié par la section de la vis, multiplié par le module d'élasticité du matériau de la vis.

Ceci n'étant valable que dans le domaine élastique, on doit vérifier que l'effort calculé divisé par la section du noyau de la vis ne dépasse pas la limite élastique de la vis. Sinon les équations ne sont pas licites.

Généralisation du cas précédent : déterminer l'effort exercé par une vis sur un assemblage de pièces élastiques en fonction du nombre de tours de serrage

On se place dans le cas où une vis serre deux pièces l'une contre l'autre. Les pièces sont donc empilées.

Lorsque la raideur des pièces n'est pas significativement plus grande que la raideur de la vis, on est obligé de tenir compte de la raideur des pièces dans le calcul de l'assemblage. En effet, si la vis s'allonge, les pièces s'écrasent de manière également élastique sous l'effet du serrage.

Si la vis a une raideur R1, la première pièce une raideur R2, la seconde pièce a une raideur R3, la raideur de l'ensemble composé de la vis et des deux pièces appelé raideur totale Rt est définie par l'équation :

1/Rt = 1/R1 + 1/R2 + 1/R3 [6]

La raideur totale est toujours inférieure à la plus faible des raideurs lorsque les pièces sont empilées.

Les valeurs 1/Rt; 1/R1 ; 1/R2 ; 1/R3 sont respectivement appelées Souplesse totale, souplesse de la vis, souplesse de la pièce 1, souplesse de la pièce 2.

Les souplesses de chaque pièce s'additionnent pour calculer la souplesse totale. Donc la souplesse totale est toujours plus grande que la plus grande des souplesses des pièces

La méthode de calcul est ensuite la même que lorsque les pièces sont supposées infiniment rigides mais on substitue la souplesse totale à la seule souplesse de la vis.

Le calcul n'étant valable que dans le domaine élastique, on doit vérifier que l'effort calculé divisé par la section du noyau de la vis ne dépasse pas la limite élastique de la vis. mais on doit aussi vérifier que cet effort divisé par la section de chaque pièce constitutive ne dépasse pas la limite élastique de chaque pièce concernée. Si ce dernier point n'est pas respecté, la ou les pièce(s) qui ne respecte(nt) pas cette condition sera (ont) plastifiée(s) et les équations ne seront plus licites.

Méthode de serrage d'une vis sans clé dynamométrique

On se propose de serrer une vis de manière à obtenir une tension de vis voisine de 80 % de sa limite élastique sans clé dynamométrique. C'est tout à fait possible en utilisant les équations ci-dessus.

Première étape : calcul de la section du noyau de la vis avec l'équation [4]

Seconde étape : calcul de la tension optimale de la vis = limite élastique x 80% x section du noyau

Troisième étape : calcul de la raideur de la vis avec l'équation [5]

Quatrième étape : calcul de la raideur des pièces serrées d'après leurs modules d'élasticité et une estimation de leurs section comprimée (ce n'est hélas pas toujours facile....)

Cinquième étape : calcul de la raideur de l'assemblage en utilisant l'équation [6]

Sixième étape : en utilisant le résultat trouvé à la cinquième étape, calcul de l'allongement relatif nécessaire pour obtenir l'effort calculé dans la seconde étape grâce à l'équation [3].

Septième étape : calcul du nombre de tours de vis nécessaire en prenant en compte le pas de la vis et sa longueur initiale.

Cette méthode peut paraître longue à mettre en œuvre. En fait c'est la base de la méthode de serrage en vigueur depuis la fin des années 80 : on effectue un faible serrage au couple (pour être sûr que les pièces plaquent bien) et ensuite on tourne d'un angle communiqué par le constructeur. L'angle donné par le constructeur ne correspond en général pas à une tension de la vis égale à 80 % de la limite élastique, mais à l'entrée dans le domaine plastique. En serrant les vis dans le domaine plastique, on assure une tension égale pour toutes les vis qui constituent un assemblage. Cela augmente la fiabilité de certains mécanismes délicats.

Mais en contrepartie, comme les vis sont étirées de manière irréversible, on n'a pas de certitude quant à la possibilité de les utiliser plus d'une fois sans entrer dans le domaine d'écrouissage. C'est pour cette raison que les constructeurs demandent aux réparateurs de mesurer la longueur des vis avant leur réemploi et si nécessaire de rebuter les vis allongées.

Ce gaspillage n'est pas obligatoire si on serre dans le domaine élastique. Et c'est pour cette raison que nous préconisons le serrage à 80 % de la limite élastique pour la majorité des assemblages. Exceptions : culasses, chapeaux de paliers, vis de bielles ou de volant d'inertie.

Méthode de serrage d'une vis avec une clé dynamométrique

Le serrage avec une clé dynamométrique est encore très employé. On parle ici de la méthode ou on applique un couple sans s'occuper de l'angle de rotation. Disons-le tout de suite, cette méthode est très imprécise. Elle est imprécise parce qu'elle dépend de paramètres qu'on ne peut ni garantir, ni facilement mesurer : les coefficients de frottement entre la tête de vis et son appui, entre les filets de la vis et ceux de l'écrou.

Pour s'affranchir en partie seulement du problème de coefficient de frottement, les meilleurs tableaux de serrage au couple prennent en compte les états de surface et la lubrification des interfaces. C'est mieux que rien mais ça reste assez peu précis. De plus, une vis réutilisée n'a plus le même état de surface qu'une vis neuve. C'est également le cas des écrous et des pièces d'appui.

L'incertitude est donc assez grande à ce niveau.

Mais il y a un autre paramètre dont on ne parle quasiment jamais dans la littérature : le pas de la vis. Tous les tableaux usuels correspondent à des vis à pas normaux. Or, avec un pas fin, la démultiplication de l'effort est différente. Une vis à pas fin serrée au couple requis pour une vis à pas gros est mal serrée.

On pourra par exemple se référer au tableaux disponibles avec ces liens :

Métrique

http://jpierre.vfl-fr.com/Fiches-Tech/Couple_de_serrage-metrique.pdf

http://www.facom.com/partage/dynamometrie/guide_serrage_controle.pdf

Impérial

http://www.abms.ca/Technique/Couple_de_serrage.pdf

Le coefficient de frottement dynamique est toujours plus faible que le coefficient de frottement statique. Les pilotes le savent bien : roues bloquées on ne dirige plus une voiture. Pour la visserie, les couples dynamiques sont également plus faibles que les couples statiques. par conséquent quand on serre avec une clé dynamométrique, il ne faut pas arrêter le mouvement avant d'avoir atteint le couple requis. Si on arrête le mouvement un peu avant d'avoir atteint la consigne, la clé déclenche lors du second serrage sans que la vis ne tourne. La clé déclenche, mais la vis n'est pas assez tendue.

Une curiosité : méthode de serrage par effet thermomécanique

La méthode suivante est citée juste pour montrer que c'est bien la tension de la vis qui compte, mais qu'avec un peu d'imagination on peut l'obtenir de différentes manières. Ici, il s'agit de la méthode de serrage des bielles de moteurs de locomotives. Sur une bielle à température ambiante, on monte les vis de bielles préalablement chauffées jusqu'à ce que les têtes portent sur le chapeau de bielle. En refroidissant les vis se rétractent et se tendent. La longueur de la vis et la température de préchauffage bien choisies suffisent pour obtenir un serrage idéal sans que les variation de coefficients de frottement puissent être la source de dispersions de tension.

Méthode de serrage généralement utilisée en Formule un et souvent en mécanique aviation

La vitesse de déplacement des ultrasons dans l'acier est connue. Envoyés par la tête de vis, les ultrasons se propagent dans la vis avant d'être réfléchis par l'extrémité de la vis et de revenir vers la tête. En mesurant le déphasage des ondes on peut mesurer la longueur de la vis. Il suffit d'obtenir le bon déphasage pour obtenir le bon allongement, donc la bonne tension de vis. L'impact des frottements n'est pas la source de divergences de tension.

Contraintes et déformations au niveau des filets en prise

Les méthodes de dimensionnement et d'obtention de la tension nécessaire décrites dans les paragraphes précédents sont basées sur un postulat : la zone la plus contrainte (celle qui cèdera en cas de surcharge) est la section perpendiculaire de la vis qui se trouve au niveau du fond du premier filet. Cela a été dit parce que vérifié par l'expérience depuis que les assemblages vissés existent. Il restait néanmoins à le démontrer. La démonstration par des méthodes analytiques nécessite des calculs complexes dont la compréhension n'est hélas qu'à la portée de mécaniciens ayant une très bonne connaissance des mathématiques. Or, ce modeste article sur la visserie n'a pas vocation de s'adresser à une population ayant "fait maths sup. et maths spé.", mais au plus grand nombre d'entre-nous. Heureusement, le calcul par la méthode des éléments finis (qui est très ancienne) allié à la puissance des ordinateurs modernes permet d'obtenir des images de synthèse qui représentent les champs de contraintes et les champs de déformation dans un assemblage fileté.

Le principe de la méthode des éléments finis repose sur un maillage des pièces à étudier. On remplace la matière d'une pièce par une sorte de treillis virtuel composé de mailles reliées par des noeuds. L'ordinateur calcule la valeur du paramètre recherche pour chaque noeud reliant plusieurs mailles. Le paramètre recherché peut être une température, une contrainte, une déformation par exemple.

Grâce au calcul numérique on peut obtenir des images où les déformations des pièces sont exagérées afin qu'ils soit beaucoup plus facile d'apprécier les zones où leur amplitude est la plus importante.

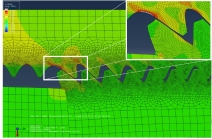
L'image qui est présentée ci-dessous nous a été communiquée par Vincent, un collègue de travail que nous remercions vivement. Vincent est responsable du service calcul d'une société d'ingénierie mécanique automobile.

Il s'agit d'une section virtuelle d'un assemblage fileté. Le travail a été réalisé avec le logiciel Abaqus.

Sur cette image de synthèse, on a représenté les déformations des filets en prise en exagérant fortement l'amplitude des déformations réelles. Les couleurs représentent l'amplitude de contrainte en chaque point. Ici, il s'agit de la contrainte dite de Von Mises. Nous n'entrerons pas dans le détail de la définition mathématique de cette contrainte, mais il faut savoir que cette représentation ne permet pas de discriminer traction et compression. Les zones peu contraintes sont représentées en bleu, puis vert pour des zones un peu plus contraintes, jaune, orange, rouge, enfin blanc pour les zones de plus en plus contraintes.

La vis est en haut, l'écrou en bas. La vis tire vers la gauche l'écrou qui s'appuie sur la pièce qu'on voit en bas à gauche. Vis et écrou bénéficient d'un maillage fin dans les filets puisque ce sont les zones où on s'attend à de gros gradients de contraintes. Le coeur de la vis et celui de l'écrou sont maillés plus gros pour réduire les temps de calcul des ordinateurs. En fonction de la finesse du maillage, certains calculs peuvent nécessiter plus d'une journée de calcul numérique. On a donc intérêt à minimiser le nombre de mailles pour réduire le temps de calcul. Mais pas trop, sinon l'ordinateur ne donnera que des valeurs moyennes. L'approche avec des valeurs moyennées est justement celle que nous avons eu jusqu'à présent dans cet article On a divisé l'effort par la surface pour connaître la contrainte moyenne. Autrement formulé, on a supposé que la matière transmettait l'effort de manière homogène ce qui est inexact. Mais cet approche est suffisante pour des pièces ne comportant pas de singularité dans la mesure où les valeurs de Re et de Rm qui sont communiquées par les sidérurgistes ont été établies aussi de manière globale. C'est toujours le cas. C'est l'expérience de l'ingénieur calcul (souvent un docteur-ingénieur) qui lui permet de définir le maillage le plus approprié. Ici, on savait que l'âme de la vis était moins contrainte que les filets parce qu'elle ne comporte pas de singularité alors que les filets constituent des singularités. Donc, le maillage a été choisi plus grossier à l'âme et plus fin dans les filets.

Le premier constat qu'on peut faire c'est qu'une fois l'assemblage serré, le pas de la vis tend à s'allonger alors que celui de l'écrou tend à se raccourcir. En amont de l'écrou, la vis s'allonge comme un ressort de section constante : de manière homogène. Mais dans l'écrou, l'allongement de la vis est moindre parce que l'écrou contribue à empêcher l'allongement de la vis. Pour cela, il subit une contrainte de compression qui tend à faire diminuer son pas.

On remarque également que dans l'écrou, les contraintes sont moindres que dans la vis. Cela correspond donc bien à ce qui a été annoncé dans la troisième partie de cet article. La zone la plus contrainte en traction se situe en fond du premier filet en prise de la vis; c'est donc à ce niveau que la matière va se rompre en cas de surcharge.

Le calcul numérique montre donc bien la zone où on constate la rupture lors d'essais pratiques.

On vient de voir que sous tension, le pas de la vis s'allonge alors que celui de l'écrou diminue. Cela a une conséquence fondamentale : l'effort transmis pas le premier tour de filet en prise est beaucoup plus important que celui transmis par le second tour lequel est plus important que celui transmis par le troisième qui est lui même plus important que l'effort transmis par le quatrième tour. Et cela se voit en termes de déformations. le pas du premier tour de filet est plus grand que le pas du second tour, lequel est plus grand que celui du troisième tour, etc. On s'arrête au quatrième tour de filet car au-delà les efforts transmis sont insignifiants. Les quatre premiers (et surtout les trois premiers) ont fait la quasi-totalité du travail.

C'est fondamental parce que cela démontre qu'il ne sert à rien d'augmenter le nombre de tours de filet en prise en pensant que ça améliorera proportionnellement la tenue des filets. C'est totalement illusoire.

Ici on était dans le cas d'une vis en acier et d'un écrou en acier. Une longueur en prise de 0,8 fois le diamètre nominal est suffisante. C'est d'ailleurs la hauteur des écrous les plus courants. Pour les taraudages, on laisse toujours une petite garde en fond de taraudage. Par conséquent dans l'acier on taraude habituellement sur une longueur égale à une fois le diamètre. Plus ne nuit pas, mais ça n'apporte pas plus de résistance au montage.

Quand la vis est en acier et l'écrou ou le taraudage en alliage d'aluminium, le comportement est différent. En effet les alliages d'aluminium ont un module d'élasticité trois fois plus faible que l'acier. La loi de répartition de charge est donc différente. Le nombre de tour de filet qui participent à la transmission d'effort est supérieur. Dans ce cas, on taraude sur 1,5 fois le diamètre.

A savoir : quand il s'agit de goujons, les profondeurs d'implantations sont majorées : 1,5 fois le diamètre dans l'acier et deux fois le diamètre dans les alliages d'aluminium.

Notion de coefficient de concentration de contraintes

Nous venons de montrer grâce à un outil moderne que la contrainte ne se répartit pas de manière homogène dans les pièces présentant des singularités. Mais bien avant l'apparition de l'informatique, on pouvait pré-déterminer le comportement des pièces en fonction des singularités de celles-ci. On dispose de tableaux et de courbes qui donnent des coefficients de concentration de contrainte (appelés Kt) en fonction des formes des pièces. Si l'utilisation de cette méthode rustique, mais assez robuste dans la plupart des cas, peut faire sourire les jeunes ingénieurs, c'est simplement parce qu'ils oublient un peu vite que le monde dans lequel ils vivent aujourd'hui a été bâti par leurs ainés avec ces méthodes rustiques. Mieux vaut souvent réfléchir et utiliser des moyens rustiques qu'on maîtrise bien plutôt que de disposer d'un arsenal de moyens ultra-sophistiqués mais de l'utiliser bêtement en avalant n'importe quel résultat dont l'aberration apparaît rapidement à celui qui réfléchit tant soit peu. Lien

L'objectif ici n'est pas de dénigrer la technologie, bien utilisée, elle permet d'aller plus loin, mais plutôt de rassurer ceux qui se sentiraient dévalorisés parce qu'ils ne connaissent pas le dernier outil "à la mode". On n'a pas besoin d'avoir le dernier "Naze-phone" pour savoir écrire...

Ceux qui veulent utiliser ces méthodes pourront se reporter au document accessible avec ce lien : Concentrations de contraintes

Un cas typique de concentration de contraintes

En dehors des zones filetées, les vis offrent un autre cas typique de concentration de contrainte : la variation brutale de section entre leur tête et leur corps. Il suffit d'observer une vis du commerce, autant ordinaire qu'elle soit, pour constater qu'il y a toujours un congé de raccordement entre la tête et le corps de vis. Son rayon a une importance capitale lorsque la vis travaille en fatigue (voir ci-dessous.) Plus le rayon est grand, plus la vis sera résistante. Observez une vis de bielle ou de culasse et vous verrez que le rayon sous tête est toujours réalisé de manière très soigné. Surtout sur les vis de compétition.

Ci-dessous, une image de synthèse issue d'une simulation numérique avec le logiciel Abaqus.

A gauche de l'image, la tête de la vis. En bas à droite, la pièce sur laquelle elle s'appuie; Au-dessus en gris, la partie du trou de passage non-occupée par le corps de vis dont on voit une partie au-dessus. Le rayon sous tête est au centre de l'image. La zone rouge est celle où la concentration de contrainte est la plus intense. C'est là que la tête cassera si la charge est trop importante ou en cas de fatigue.

Un grand rayon peut cependant être gênant pour la portée de la tête. On est parfois obligé de réaliser un gros chanfrein à l'entrée du trou pour assurer une bonne portée à la tête.

Quand on ne peut pas améliorer la dimension du rayon, on peut le réaliser en rectification pour éliminer les stries d'usinage qui sont des concentrations de contraintes par nature. On peut aussi galeter ce rayon, comme on galette les manetons de vilebrequins pour en améliorer la tenue en fatigue par effet d'écrouissage. C'est évidemment une affaire de spécialiste et cette pratique est très répandue pour la visserie aéronautique.

Cas des assemblages qui travaillent en fatigue

Tout ce qui a été dit plus haut à propos du dimensionnement des vis n'est valable que pour les assemblages qui ne travaillent pas en fatigue, c'est-à-dire pour des assemblages dont le chargement est constant. Par exemple, une vis qui supporte sans mouvement un contrepoids dont la masse n'évolue pas.

Pour les assemblages qui travaillent en fatigue, c'est-à dire pour ceux dont la charge évolue de manière cyclique, par exemple une bielle dont la tête est tantôt comprimée tantôt tirée, on doit tenir compte du risque de rupture en fatigue dans le dimensionnement.

L'approche la plus simple est d'utiliser les courbes de Wohler. Ces courbes permettent de définir un facteur de sécurité qui permet de minorer la limite élastique d'un matériau utilisée dans les calculs ci-dessus pour que l'assemblage soit pérenne. Plus le nombre de cycles sera grand, plus le facteur de minoration le sera également.

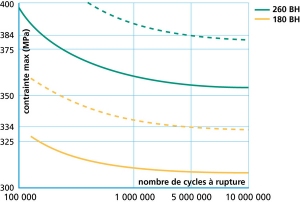
Ci-dessous, quelques courbes de Wohler fournies par Arcelor Mittal pour les aciers 180BH et 260 BH de leur production.

L'acier 260 BH peut être utilisé en fatigue jusqu'a 400 MPa pour moins de 100 000 cycles, 360 MPa jusqu'à 1 million de cycles, 355 MPa pour 10 millions de cycles ou plus.

Il existe d'autres méthodes, plus précises que l'utilisation des courbes de Wohler car elles tiennent compte de l'amplitude de la variation de la sollicitation. Leur usage découle d'une approche nettement plus professionnelle que celle des courbes de Wohler aujourd'hui dépassé pour des assemblages vissés très sollicités comme, par exemple les vis de bielle.

Ceux qui sont intéressés par ces approches plus précises pourront trouver sur Internet des renseignements sur, par exemple le critère de Dang Van ou les diagrammes de Haigh ou Goodman. Ces méthodes permettent de définir un coefficient de sécurité (safety factor) assez précis.

Ceux qui au contraire cherchent à dimensionner de manière pragmatique des montages simples dont la défaillance ne peut pas être à l'origine d'un accident peuvent se contenter de diviser la limite élastique du matériau par deux. Attention, cette approche n'est pas applicable pour les éléments susceptibles d'avoir un impact sur la sécurité.

Merci de leur attention aux courageux qui sont allés jusqu'au bout de cet article n'hésitez pas à poser des questions si quelque chose ne paraît pas clair.

Le savoir n'a de valeur que s'il est partagé par tous.

TRD CARS are lubricated by RED LINE